Il Solaria Horologia di Juan Caramuel
I QUADERNI DELLA SOCIETÀ STORICA VIGEVANESE
Numero 5
Guido Cazzani
L’opuscolo di Jujan Caramuel, intitolato Solaria Horologia da un moderno bibliotecario, forse mons. Francesco Pavesi, si trova nella Biblioteca Vescovile di Vigevano, in una cartella che contiene anche un’altra opera di Juan Caramuel, l’Epistola de horologiis, di ben maggiore estensione, almeno per quanto riguarda il numero di pagine. Solaria Horologia è infatti conservato come manoscritto, in parte di mano dell’autore Juan Caramuel, in parte di mano di un ignoto copista, ed occupa in tutto nove facciate, delle quali quattro bianche e tre incomplete, a fronte delle 46 facciate dell’Epistola de horologiis, scritte, da un ignoto copista, a doppia colonna più il frontespizio, come si legge in un’annotazione manoscritta a matita sul fascicolo.
Mentre l’Epistola de horologiis tratta un caso che potremmo sicuramente definire di protezione della proprietà intellettuale, che con riferimento alla legislazione attuale ed al linguaggio attuale potremmo definire di brevetti nel settore dell’orologeria, Solaria Horologia tratta la precisione ed affidabilità degli orologi in funzione del loro uso per le osservazioni astronomiche.
In Solaria Horologia Caramuel si serve di numerose citazioni da autori come Witekind, Alsted, e soprattutto Brahe, tutti protestanti, mentre nell’Epistola de horologiis, che riguarda un caso che doveva essere trattato alla corte pontificia, cita quasi esclusivamente autori cattolici, anche quando questi hanno ben poco di valido da dire nel settore tecnico e scientifico: evidentemente la capatatio benevolentiae della corte pontificia, per ottenere un risultato favorevole a Eustachio Divini, a cui causa Caramuel patrocinava, aveva consigliato quella scelta.
Proprio la presenza delle due grafie, molto ben distinguibili, e le correzioni apportate al testo, hanno permesso a chi scrive queste brevi note di identificare senza ombra di dubbio quale fosse la grafia di Caramuel: le correzioni infatti modificano il testo e la sua esposizione, inseriscono ed eliminano brani di testo, e possono essere opera solo dell’autore dell’opera. Per sostituire parti di testo, o per inserirne di nuove, Caramuel ha fatto ricorso ad operazioni di taglia ed incolla, tagliando ed incollando, letteralmente, pezzi di foglio.
Nel manoscritto non è indicato dove finiscono le citazioni, ed un confronto con i testi originali, reperiti presso il Münchener Digitalisierungszentrum della Bayerische Staatsbibliothek, ha permesso di osservare che alla mano del copista sono dovute solo le citazioni: probabilmente Caramuel aveva ritenuto opportuno risparmiare il suo prezioso tempo, affidando al copista il banale compito di copiare le citazioni. Per alcune di queste citazioni, come quelle da Witekind, da Alsted, e dai Progymnasmata di Brahe, il confronto con i testi originali ha permesso di trovare leggeri scostamenti nella punteggiatura e nella grafia di alcune parole, oltre ad alcuni errori.
Caramuel inizia con una breve trattazione sull’antichità degli orologi solari (fig. 1), interamente presa da un’opera di Hermann Witekind (fig.2), il cui nome è, almeno nella prima citazione, storpiato in Wirekind.

| fig. 1 |
| Trattazione manoscritta sull’antichità degli orologi solari. |

| fig. 2 |
| Hermann Witekind, frontespizio del Conformatio horologiorum sciotericum. |
Già in questa prima citazione si trovano più errori, in particolare per il fatto che, ad un certo punto, si arriva alla citazione della citazione della citazione: Witekind cita un passo delle Donne al parlamento (Le ecclesiazuse) di Aristofane, attraverso una citazione di Aristofane contenuta nell’Onomasticon di Giulio Polluce (fig. 3). Il testo greco, citato nel testo di Polluce (fig. 4, ultime righe della pag. 271), è già poco comprensibile nella citazione di Witekind (fig. 5), ed ha potuto essere corretto ritrovando il verso delle Donne al parlamento (Ecclesiazusae) di Aristofane, che recita : ὅταν ᾖ δεκάπουν τὸ στοιχεῖον, λιπαρὸν χωρεῖν ἐπὶ δεῖπνον. Il senso è comunque esattamente quello che Caramuel riprende da Witekind e da Polluce: quando l’ombra dello gnomone sarà di dieci piedi andrai a cena unto e lavato.

| fig. 3 |
| Onomasticon di Giulio Polluce. |

| fig. 4 |
| Onomasticon di Giulio Polluce. |

| fig. 5 |
| La citazione di Caramuel, dalla Conformatio Horologiorum Sciotericorum di Witekind, inizia da questa pagina “Itaqe inde usq; à priscis seculis…”. La citazione dal testo greco delle Ecclesiazuse di Aristofane (in Concionatricibus) inizia alla dodicesima riga dal fondo. |
Nella breve opera Caramuel esamina i principali difetti degli orologi meccanici della sua epoca, in particolare per il loro impiego nelle osservazioni astronomiche, comparandoli con i vantaggi offerti dall’uso degli orologi solari, da Caramuel detti anche “sciatherici”, dal greco σκιά (ombra).
Il titolo Solaria Horologia deve essere stato attribuito prendendolo dall’espressione “solaria horologia”, che compare nella prima riga del testo, ma l’annotazione in margine a sinistra[1], chiaramente di mano del Caramuel, reca un “De sciatherici antiquitate”, ossia “sull’antichità dello sciaterico”, essendo gli sciaterici gli orologi ad ombra, intendendosi per ombra quella dello stilo o gnomone, che caratterizza ancor oggi le meridiane.
Il testo non è databile, se non per un probabile termine post quem, che compare al foglio 27r, dove Caramuel afferma “erant anno XLVI Pragae in arce…”: l’anno doveva essere il 1646, stante il riferimento ad orologi raccolti dall’imperatore Rodolfo II, che fu Imperatore del Sacro Romano Impero dal 1576 al 1612. Non si trovano termini ante quem, e non sono ricavabili altri termini post quem dalle citazioni di studiosi dell’epoca di Caramuel o precedenti, alcuni molto noti come l’astronomo danese Brahe, altri meno noti come Alsted e Witekind.. Le citazioni dagli antichi sono poche, e sono contenute nella prima citazione da Witekind: il libro 4 dei Re dalla Bibbia, Valerio Massimo, Luciano di Samosata ed Aristofane.
Il modello del sistema solare adottato da Caramuel è sostanzialmente quello geocentrico di Brahe, da Caramuel stesso disegnato nel foglio 28r, corredando il disegno con esaurienti didascalie (fig. 6). Caramuel, nell’altra sua opera “Epistola de horologiis”, conservata nella Biblioteca Vescovile di Vigevano insieme al presente testo, fa esplicito riferimento alle teorie eliocentriche, ed in particolare a quelle di Galilei e di Copernico, per le quali rammenta in più di un punto la condanna da parte della chiesa cattolica. Caramuel sceglie quindi in questo testo, senza però darne una giustificazione, il sistema geocentrico di Brahe, ammesso dalla chiesa cattolica, quello stesso del quale afferma, nel foglio 21r dell’Epistola de horologiis, che è il sistema che rimane dopo che la chiesa cattolica ha condannato i sistemi di Copernico e di Galileo[2], e del quale ammette tuttavia le difficoltà
——————————————————————————————————————–
[1] Le annotazioni a margine sono molto usate da Caramuel
[2] Il testo nell’Epistola de horologiis, al foglio 21r, è: “Ergo remanet systema illud, quod cogitavit Tycho, in cuius mechanicâ conformatione tantas difficultates et remoras repererunt artifices, ut multi thesim distinguant ab hypotesi et tametsi illam conforment resolutioni ecclesiae, hanc Copernico attemperant, ut planetarum circulus facilius et exactius promoveant”.
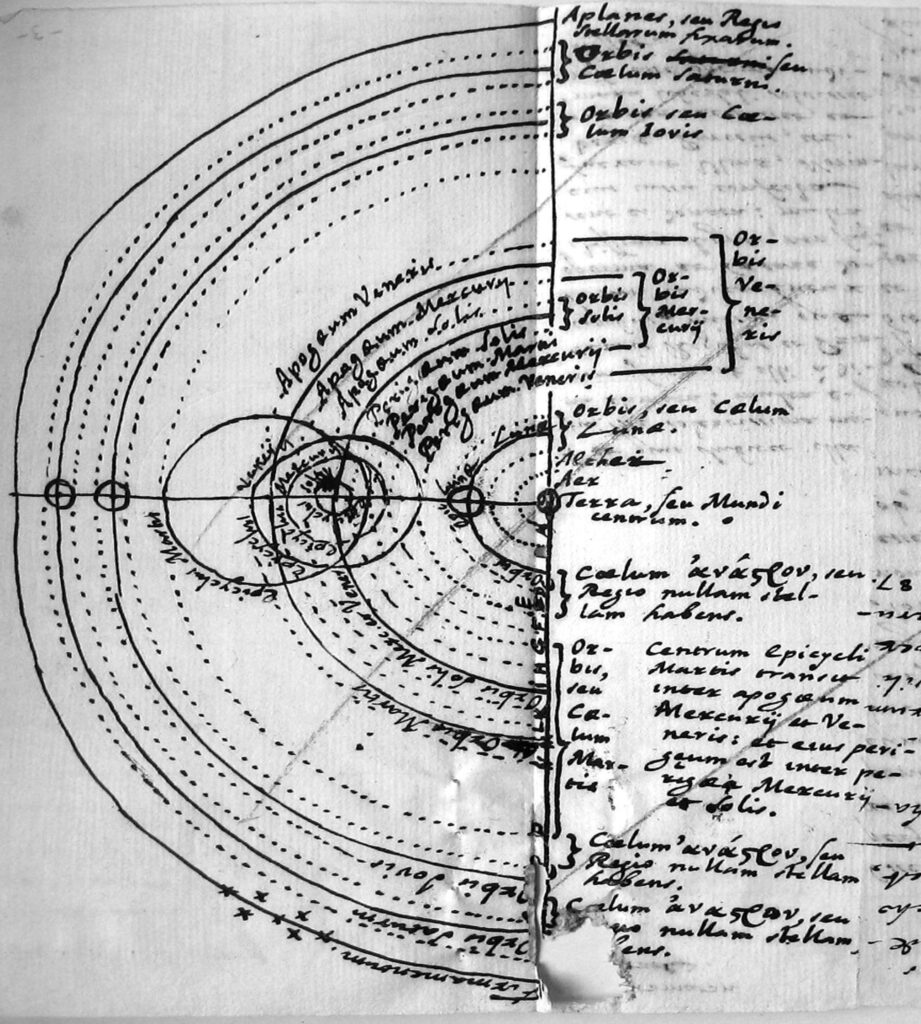
| fig. 6 |
| Il disegno è annotato con scritte autografe di Caramuel; essendo la grafia di Caramuel difficile da decifrare, si riportano la trascrizione e la traduzione in allegato. |
Numerose sono le osservazioni più tecniche che scientifiche nel presente testo, alcune addirittura sorprendenti per un lettore moderno che, se possiede una formazione tecnico scientifica, è abituato a separare le questioni puramente tecniche, di tipo pratico, da quelle scientifiche di tipo prettamente teorico: si vedano, ad esempio, la trattazione e la figura della posizione e della giacitura dell’orologio mosso da pesi, nel foglio 34v (fig. 7).
| fig. 7 |
| Figura della posizione e della giacitura dell’orologio mosso da pesi. |
Alcune delle osservazioni di Caramuel che possono sembrare oggi in parte ovvie, in parte errate, alla luce delle conoscenze scientifiche sviluppate nei secoli successivi a questo scritto, non lo erano affatto all’epoca di Caramuel: non dimentichiamo che Caramuel scriveva prima che fossero noti il calcolo differenziale, l’equazione fondamentale della dinamica, i concetti di attrito, di accelerazione, di energia cinetica, di quantità di moto.
Nel presente scritto Caramuel usa alcune parole tecniche come lo spagnolo “muelle”, per spiegare e indicare quella che oggi chiamiamo molla, che Caramuel chiama latinamente “lamina” o “spira”.
Le citazioni costituiscono una parte notevole del testo dell’opuscolo, che è redatto in un latino privo di fronzoli, molto diverso da quello dell’Epistola de horologiis, ed è rivolto ad un Federico che non sembra identificabile. Tutti i disegni sono posti nelle pagine contenenti scrittura autografa, e devono quindi ritenersi, anche per la grafia delle didascalie, opera autografa di Caramuel. Dell’opuscolo di Caramuel, ancora inedito, l’amico ing. Alessandro Scandella fotografò il testo manoscritto: sulla base di quelle prime fotografie che a lui devo, e di altre eseguite in seguito per risolvere dubbi ed incertezze di interpretazione, legati a pieghe e strappi della carta, ho eseguito una trascrizione, e la traduzione qui allegata.
Le figure n. 8 e n. 9 rappresentano il recto ed il verso del foglio 34, con le illustrazioni autografe del Caramuel.

| fig. 8 |
| La figura rappresenta il foglio 34 r, con le illustrazioni disegnate dal Caramuel |

| fig. 9 |
| La figura rappresenta il foglio 34 v, con le illustrazioni disegnate dal Caramuel |
Orologi solari
Juan Caramuel
pag. 1 (foglio 26r, numero in basso a sin.)
Chiedi quanto siano antichi gli orologi solari: ed io per non affaticare me o te collazionando ed esaminando vari autori, cito le parole e i detti di Hermann Wirekind[1], che infatti, all’inizio del libro che è detto Conformazione degli orologi sciaterici, così scrive[2].
Pertanto fin dai primi secoli sempre presso i popoli più civilizzati e colti è stato usato qualche metodo di questa divisione oraria. Delle quali la più antica e principale pare l’orologio sciaterico o solare, nel quale l’ombra, proiettata dal sole autore del giorno dallo stilo o gnomone, distingue le ore toccando le linee sottostanti che incontra. Di orologio di questo tipo la prima menzione è nella storia sacra, libro 4 dei Re, dove si legge che a Gerusalemme nella meridiana, fatta dal re Achas, l’ombra per volontà di Dio, in grazia dell’ammalato Ezechia mirabilmente retrocesse per dieci linee. Il re Achas però regnò 3210 anni dopo che il mondo era stato creato: 2320 anni prima della nostra era. Si narra che Anassimene mostrasse il primo [orologio] sciaterico pubblicamente ai Lacedemoni all’inizio del regno di Ciro, che fu nel duecentesimo anno dopo il regno di Achas. Consta che presso gli Ateniesi orologi di questo tipo fossero stati diffusi già al tempo della guerra peloponnesiaca. Poichè da Aristofane, che visse a quel tempo, fu scritto nelle “Donne al parlamento”: ὅταν ᾖ δεκάπουν τὸ στοιχεῖον, λιπαρὸν χωρεῖν ἐπὶ δεῖπνον[3]. Dove ci sia stata un’ombra di dieci piedi, andrai lavato ed unto a cena. Στοιχεῖον (per dichiararlo incidentalmente) è per Polluce[4] l’ombra dello stilo. In δεκάπον sembra che πους
NOTE A MARGINE
S in alto: Sull’antichità dello sciaterico
pag. 2 (foglio 26v)
indichi i singoli intervalli delle linee, per quanto disuguali: ciò che si può anche dedurre anche da Micyllo e Cronosolone di Luciano: i quali intervalli, poiché erano dodici, secondo il numero di ore di tempo allora usate, sono rappresentati qui dalla decima ora dall’inizio del giorno artificiale (quello che chiamano così) e dalla terza prima della fine. A Roma fu collocato pubblicamente il primo orologio solare, durante la prima guerra punica, portato dalla Sicilia tre le spoglie di Catania saccheggiata: ma rozzo e poco in accordo con le ore. Al tempo di Cicerone sembra che il loro uso già si fosse poi diffuso da questo fatto, che poco prima che egli stesso fosse trucidato nella sua villa di Gaeta, un corvo aveva fatto cadere a terra il ferro dell’orologio, per predire l’imminente sua uccisione: come tramandò alla memoria Valerio Massimo ben centocinquant’anni prima di Cicerone, in una certa favola plautina, raccolta da Gellio, un parassita affamato, e quindi desiderante che per ognuno sia orologio il suo ventre, maledice la moltitudine di orologi solari nella città[5].
pag. 3 (foglio 27r, numero in basso a destra)
Supponi temerariamente (Federico[6]) che gli automi o orologi a ruote siano perfetti ed esatti, e che gli uomini debbano necessariamente fidarsi di essi: infatti nessuno zelo di un artefice nel perfezionare, né la cura e la diligenza di alcuno nel regolare poté arrivare o a fabbricare un orologio perfetto, o a regolarlo bene ed in modo esatto. D’altra parte, coloro che confidano negli orologi, non devono essere chiamati astronomi, infatti misurano una cosa che deve essere certissima (appunto il tempo delle osservazioni) con una misura[7] assai incerta.
L’esperienza quotidiana conferma questa mia opinione; e infatti la maggior parte degli orologi, che sono detti ben regolati, presentano differenze e deviano: se infatti non deviassero, sarebbero in accordo tra loro. Molti e diversi ne raccolse l’imperatore Rodolfo II: e chi dubiterebbe che quelli fossero stati elaborati da una mano abilissima? Molti furono infatti a lui mandati da diversi re e principi, che se non fossero giudicati ottimi e degni di un imperatore dottissimo, non sarebbero stati a lui donati: per suo ordine ne erano stati fabbricati molti a Ulma, a Norimberga, a Parigi, ecc., che non avrebbe accettati, e pagati generosamente, se non li avesse giudicati ottimi. Erano nell’anno XLVI[8] a Praga nella fortezza, e disposti in lunga fila di qua e di là ed in mezzo, occupavano ed ornavano un’aula (comunemente, una galleria) che da questi stessi apparecchi prendeva nome ed era detta orologiaria. Ma in tanto grande e tanto varia moltitudine di orologi, a stento ce ne erano due, che andassero d’accordo: a stento uno che rappresentasse l’ora dell’orologio sciaterico.
pag. 4 (foglio 27v)
Da qui viene che gli uomini dotti ed esperti non vogliono dipendere dagli orologi nelle loro osservazioni: e poiché Tycho Brahe è un astronomo celeberrimo, cito lui. Egli non volle mai fidarsi degli orologi a ruote[9], e considerava un miracolo o un prodigio, se qualche volta erravano di poco: poiché sembra che sia una loro inevitabile caratteristica quella di errare molto. Di quanto in bassa considerazione fossero sempre stati tenuti presso di lui gli automi[10] ci convince una curiosa ed erudita lettera datata Uraniborg 18 gennaio 1587[11]
pag. 5 (foglio 28r, numero in basso a destra)
FIGURA SULLA PARTE DESTRA DEL FOGLIO, che dovrebbe rappresentare il sistema solare nella concezione di Brahe ( con scritte capovolte rispetto al testo della parte sinistra, che è il 27v); trascrizione sulla colonna sinistra,.traduzione sulla colonna destra.
Sul margine destro della figura, dall’alto:
Aplanes, seu regio stellarum fixarum. Regione delle stelle fisse
Orbis Saturni seu caelum Saturni. Orbita di Saturno o cielo di Saturno
Orbis seu caelum Iovis. Orbita o cielo di Giove
Orbis Solis. Orbita del Sole
Orbis Mercurij Orbita di Mercurio
Orbis Veneris. Orbita di Venere
Orbis seu caelum Lunae. Orbita o cielo della Luna
Aether Etere
Aer Aria
Terra, seu Mundi centrum Terra, o centro dell’universo
Caelum ἀνάστρον, seu regio Cielo ἀνάστρον, o regione
nullam stellam habens. che non ha nessuna stella
Orbis, seu caelum Martis Orbita o cielo di Marte
Centrum epicycli Martis transit Il centro dell’epiciclo di Marte passa
inter apogaeum Mercurij et tra l’apogeo di Mercurio e
Veneris: et eius perigaeum est quello di Venere: e il suo perigeo è
inter perigaeà Mercurij et Solis. tra i perigei di Mercurio e del Sole
Caelum ἀνάστρον, seu regio Cielo ἀνάστρον, o regione
nullam stellam habens. che non ha nessuna stella
Caelum ἀνάστρον, seu regio Cielo ἀνάστρον, o regione
nullam stellam habens. che non ha nessuna stella.
Sui semicerchi, a partire dal più esterno:
Firmamentum Firmamento
Orbis Saturni. Orbita di Saturno
Orbis Iovis Orbita di Giove
Sui cerchi, a partire dal più esterno:
Epicyclus Martis Epiciclo di Marte
Epicyclus Veneris Epiciclo di Venere
Epicyclus Mercurii Epiciclo di Mercurio
Epicyclus Solis Epiciclo del Sole
Di nuovo sui semicerchi, a partire dal più esterno:
Orbis Martis (a sinistra) Orbita di Marte
Apogaeum Veneris (a destra) Apogeo di Venere
Apogaeum Mercurij (a destra) Apogeo di Mercurio
Orbis Solis Merc. et Vener. (a sinistra) Orbita del Sole di Mercurio e di Venere
Apogaeum Solis (a destra) Apogeo del Sole
Perigaeum Solis (a destra) Perigeo del Sole
Perigaeum Martis (a destra) Perigeo di Marte
Perigaeum Mercurii (a destra) Perigeo di Mercurio
Perigaeum Veneris (a destra) Perigeo di Venere
Orbis Lunae Orbita della Luna
Epic Lunae (sul cerchio) Epiciclo della Luna
pag. 6 (foglio 29r, numero in basso a destra)
(prime 6 righe cancellate)
nella quale si meraviglia che Guglielmo langravio d’Assia facesse uso di un orologio che non errava se non di cinque o sei minuti. Le sue parole sono queste. [E non posso meravigliarmi abbastanza che la Tua Altezza abbia toccato con i suoi strumenti quasi i luoghi delle stelle, particolarmente quando posso dedurre che la Tua Altezza in Aldebora[12], o in qualunque altra abbia usato come fondamento, abbia rilevato la sua ascensione retta dal transito per il meridiano, avendo trovato il tempo per mezzo di un orologio e un confronto con il Sole. Metodo che a me veramente sembrava sempre meno sicuro: sebbene infatti io abbia quattro orologi di questo tipo di diverse grandezze, e di accurata costruzione, che indicano non solo i singoli minuti primi, ma anche i secondi; tuttavia in un tanto preciso procedimento ritenni che fosse senza fondamento prestare fede ad essi; poiché 4 secondi, che in più ore facilmente sfuggono, inducono un errore di un primo in longitudine. Aggiungi, che questi orologi anche se diligentissimamente costruiti in oricalco[13], sono sensibilmente soggetti alle mutazioni dell’aria: taccio il fatto che il peso non è uguale, quando pende più in alto e più declive,
pag. 7 (foglio 29v)
a causa della variazione della lunghezza della fune con la quale è legato, che aggiunge successivamente al peso qualcosa, che per quanto sia minimo, tuttavia apporta una deviazione non trascurabile nei secondi].
Per questa causa Tycho respinge dalla Paediâ Astronomicâ gli orologi a ruote, come inutili: e nei suoi Progymnasmati: appunto capitolo 2 del primo libro pagina 148 secondo l’edizione di Uraniborg, così dice. [In questo soprattutto consiste la difficoltà di questo procedimento, che l’istante di tempo, quale qui si richiede espresso perfino negli stessi secondi, non si può ottenere in modo così accurato, come è necessario; sebbene anche la posizione del Sole conosciuta in modo non esatto, o mediante l’osservazione, o anche mediante qualche valido calcolo, che non era prima disponibile, non poco ostacoli in questo luogo: onde è molto più appropriato usare questa procedura, intorno ai transiti equinoziali, poiché la posizione di tutto il Sole si ricava dall’osservazione, attraverso la declinazione molto variabile. E per quanto allora sia l’Illustrissimo predetto principe che io in questo ci fossimo applicati moltissimo, per far realizzare alcuni orologi perfezionatissimi, indicanti non solo le ore, ma anche i minuti primi e secondi, con legge costante, dei quali hai a disposizione tre o quattro, fatti con la massima diligenza; tuttavia per molte
pag. 8 (foglio 30r, numero in basso a destra)
cause, delle quali ho trattato per lettere anche con l’Illustrissimo principe, come sarà evidente nel libro delle Epistole Astronomiche, questi non possono essere così precisi e corrispondenti alla legge celeste perpetuamente in ogni tempo e con uguale corso, come è necessario in una così precisa attività. Infatti per quanto quegli orologi siano costruiti con l’opera e l’abilità di qualsiasi solerte artefice, tuttavia sono soggetti a mutazioni a causa del variare dei venti e dell’aria; né si sana
questo inconveniente, se siano conservati al caldo nel tempo invernale in qualche locale riscaldato anche in modo costante per quanto è possibile: per loro stessi spesso, per quanto dall’origine diligentemente costruiti, (sono) soggetti a qualche alterazione per varie cause e facilmente può accadere che un certo numero di dentini o rotelle in qualche zona disuguali, turbino di poco l’armonia del moto continuamente costante e proporzionale, e nelle ore intermedie e nelle loro minime particelle aggiungano qualche parte di irregolarità, quantunque universale, e la reintegrazione giornaliera, valutata sia rispetto al Sole che rispetto alle stelle, risulti abbastanza esatta; certo anche il filo stesso al quale il peso è attaccato, quando
pag. 9 (foglio 30v)
è lasciato scendere al massimo, aggiunge alquanto più di peso, per quanto sia sottile, che quando il peso stesso nella posizione superiore abbia tratto verso il basso una parte minima di esso filo: e sebbene questo implichi una molto esigua differenza nel moto dell’orologio, tuttavia quando intendiamo ricercare quanto sia finissima questa cosa, e una deviazione di quattro secondi nell’orologio introduca una perdita di un intero minuto primo nella posizione della stella, non manca di ogni impedimento. Ci sono anche altre cose che diminuiscono in tutto la fiducia nella precisione ed affidabilità, che è necessaria agli orologi.
È in accordo con sé stesso Tycho Brahe, che nella lettera a Rothmann del 20 gennaio 1587 così dice. In questi tempi da misurare senza dubbio in modo finissimo, non fidarti troppo dell’orologio, se esso non conserva in modo esattissimo i tempi di rivoluzione e non procede in modo uniforme in tutte le ore intermedie, e non mostra i singoli minuti contemporaneamente ai secondi separatamente.
Quali (orologi) non dubito che l’Illustrissimo Principe abbia a disposizione, avendo un costruttore di automi tanto ingegnoso ed eccellente. Anche dalle altitudini delle stelle questa precisa prassi[14] non riesce abbastanza agevolmente, soprattutto se si elevano alquanto vicine al meridiano e non mancano di errori a causa di inconvenienti di rifrazione vicino all’orizzonte. Più pratico pertanto sarebbe stato ricercare questi momenti di tempo dagli stessi azimut delle stelle, purché la linea meridiana fosse stata diligentemente osservata prima non a partire dal Sole, ma dalle stelle, in primo luogo certamente dalla stessa stella polare, quando è dall’una e dall’altra parte verso il sorgere e il tramonto dal polo, nel massimo allontanamento azimutale (procedimento che non è soggetto neppure al minimo errore, e agevolmente può essere eseguito);[15] io sono solito ottenere facilissimamente momenti di tempo esatti per mezzo di armille equatoriali, che misurano le distanze del Sole e delle stelle dal meridiano nello stesso equatore, che è la misura dei tempi, in qualsiasi luogo sorgano, al di qua di ogni sospetto di errore. Se ci accadrà di osservare i tempi esattissimi delle eclissi lunari, che si attendono in questo e nel prossimo anno, col favore divino da entrambe le parti, daremo notizia sugli intervalli dei meridiani e sui moti della Luna. Si deve però notare, che nell’eclissi totale con ritardo, meglio si distingua il tempo dell’ingresso di tutto il corpo della Luna nell’ombra terrestre, e della sua prima uscita, che i rimanenti due momenti del primo inizio e della fine ultima poiché a quelli si deve prestare più accurata attenzione.
pag. 10 (foglio 32r, numero a margine in basso a destra)
Io non accuso così gli orologi di imprecisione, per approvare tutto quello che si dice contro di essi. Per questo motivo propongo di esaminare le parole di John Alsted, che sostiene la mia opinione, ma la dimostra male. Egli stesso pertanto nel libro 30 sez. 4 §. 3. pag. 684 della sua Enciclopedia, per provare che non ci si debba fidare degli orologi, così dice[16].
L’invenzione degli orologi meccanici[17] è attribuita a Severino Boezio, sommo filosofo; degna certamente di ammirazione, per lo squisito acume, e per l’utilità inestimabile nelle attività pubbliche e private degli uomini. Del resto come nelle altre opere umane anche molto saggiamente pensate, così negli orologi sono mostrati non piccoli difetti da insigni matematici, non solo a causa delle frequenti mutazioni dell’aria dell’ambiente, ma anche a causa del principio interno del moto se così lo si può chiamare. Ci sono infatti due tipi di orologi; alcuni mossi da se stessi e soltanto da rotelle, altri invece da pesi appesi. Dei quali quelli che sono mossi dall’avvolgimento di una certa lamina violentemente attorta, per questo motivo indicano le prime ore più brevi, le ultime invece più lunghe del giusto; e questo poiché, dato che quella lamina attorta si srotola quasi per l’innata forza del metallo, per questo motivo prima muove le rotelle dell’orologio più velocemente, poi più lentamente. Mentre gli altri orologi che sono mossi da pesi appesi, indicano le prime ore più lunghe del giusto, le ultime più brevi: poiché appunto i pesi quando più sono vicini[18] al loro luogo naturale, appunto la terra, si muovono più celermente, poiché ogni moto naturale nella parte finale è più veloce che in principio. Si aggiunge anche il peso di questa fune alla quale i pesi sono legati, dal quale i pesi verso la fine sono spinti verso il basso più che all’inizio[19].
NOTE A MARGINE
S in alto: Sulla costanza (affidabilità) non tutto quello che si dice sugli orologi è vero[20]
pag. 11 (foglio 33r)
Rammentiamo, se pare conveniente, quello che dissi per compendio. Trovo quattro asserzioni. La prima è che gli orologi meccanici furono inventati da Boezio. La seconda, quelli che si caricano per torsione di lamine indicano le prime ore più brevi, e le successive più lunghe. La terza, che i pesi quanto più sono vicini alla terra tanto più velocemente e potentemente muovono le ruote. Quarta, la fune quando i pesi sono abbassati aumenta il peso, e fa sì che la macchina giri più veloce. E tutte queste cose devono essere esaminate per soddisfare la curiosità.
Che Boezio fosse dotato di felicissimo ingegno risulta dai suoi libri; non negherò che fosse uno che avrebbe potuto inventare gli orologi meccanici: ma non dirò che li abbia inventati: sembra infatti che fossero molto più antichi. Gli antichi comparavano gli orologi con i detti dei filosofi, e di qui a là sostenevano argomenti, dicevano, ci sarà accordo prima tra gli orologi, che tra i filosofi: o anche ci sarà accordo prima tra i filosofi, che tra gli orologi. Seneca (si serve) di questo modo di dire: di questo si servono altri più antichi. Ma, se sotto il nome di orologi intendessero soltanto quelli solari, a torto avrebbero insistentemente sostenuto il disaccordo: infatti tutti gli sciaterici, che siano fatti bene, non possono essere in disaccordo tra loro. Pertanto oltre agli sciaterici, un tempo anche gli antichi ebbero orologi a ruote.
Ma quando iniziarono questi? Hermann Witekind[21] nel libro sul creare sciaterici afferma che l’invenzione degli orologi meccanici non è molto antica:
pag. 12 (foglio 33v)
subito infatti dall’inizio §. del resto così dice[22]. Per ingegno mirabile ed arte esistettero (orologi) sonanti che costruiti con molte e diverse rotelle, e mossi da pesi, battono campane sospese in alte torri, così indicando le ore a tutti i villaggi e alle città. Incominciarono anche di recente ad essere fatti alcuni di questo genere, mossi da corda o da lamina flessibile, a tal punto sottili e piccoli, che possono essere portati in giro in tasca o alla cintura, come quelli solari, che popolarmente chiamano compassi[23], nei quali le ore si segnalano con quella linguetta mobile che mostra il polo, anche a quegli stessi che non sono nati da molti secoli, non appena sia percepita quella ammirevole natura del magnete che tende all’orsa (anzi anche, e qualcuno con più forza, all’austro).
pag. 13 (foglio 34r)
Le lamine che sono caricate per avvolgimento[24] (che da noi[25] sono dette muelle), produrrebbero inoltre ore disuguali, e le prime più brevi delle successive, se non vi si opponesse in due modi un provvedimento meccanico[26]: provvedimento che o ponendo un vincolo, o tirando la corda su un asse asimmetrico elimina questa irregolarità. In primo luogo infatti alla spira (così la lamina avvolta (muella) suole essere chiamata) aggiunsero la ruota ABC, che fosse premuta dalla costola AEF, fermata in F[27]. da un sufficiente numero di spine. Poi per il moto avanzante della spira si muove la ruota ABC, ma viene più frenata all’inizio in A, che in B: più in B, che in C. Pertanto quella irregolarità affermata e rimproverata dagli avversari viene ricondotta con forza e ragione alla regolarità di questo vincolo[28] AEF.
In secondo luogo aggiungono una corda, affinché la spira IK applichi un momento torcente[29] all’asse GH. Il quale asse è inoltre piramidale[30], e poiché la corda dista dal centro meno in H che in G ha bisogno di maggiore forza in H per essere messo in movimento. Pertanto se la spira (el muelle) ha maggior forza all’inizio e minore alla fine, ne richiede anche maggiore per azionare in H, che in G, e così questa irregolarità viene ricondotta alla regolarità.
Ammetto che è difficile elaborare e modellare o quell’asse piramidale GH, o quel vincolo ABC in forma di corda, affinché abbia una riduzione né maggiore né minore di quanto deve: ma nessuno negherà che è umanamente possibile, se si usa la necessaria diligenza. Per ora si omettano entrambe le correzioni, e l’indice percorra in tempi uguali archi disuguali (maggiori all’inizio, minori alla fine). Non li percorrerà forse oggi e domani nello stesso modo? (nello spazio di molti mesi la differenza è impercettibile). Pertanto se al mattino e alla sera sarà teso
pag. 14 (foglio 34v)
e caricato[31], si segni in un giorno in qual modo scorra[32] e l’orologio sarà esatto. Questo modo di segnare le ore, manca di qualunque regolarità: infatti se per caso la stessa lamina in mezzo fosse o più spessa o per caso più fortemente temprata così che misuri la prima ora con un arco minore che la successiva, o al contrario, questa stessa irregolarità potrebbe essere annotata, e non potrebbe indurre alcun sospetto di errore[33].
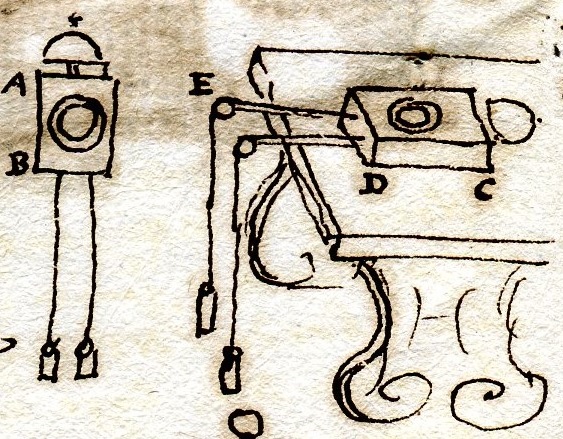
Quei meccanismi, che sono mossi da una molla a spirale, sono più belli e più comodi, non più sicuri: più comodi, poiché possono stare in tasca, in una borsa, dovunque, e non richiedono necessariamente alcun posizione: mentre invece quelli, che sono mossi da pesi, devono stare in un luogo determinato, né possono cambiare in modo comodo la posizione; se infatti volessi convertire il meccanismo AB, che è verticale e perpendicolare, in orizzontale (imponendo appunto che sia appoggiato su una mensola, come in CD) dovresti aggiungere le rotelle E, per fare scendere attraverso esse i pesi[34].
Alsted imputa a questi meccanismi l’irregolarità, poiché il moto dei gravi verso la fine è più veloce, ed i pesi quanto più sono più vicini alla terra, sono più pesanti. Certamente di questi due ragionamenti il primo non è pertinente, ed il secondo suppone il falso. Il primo non è pertinente, poiché i pesi non muovono il meccanismo con una spinta secondaria ma con la loro sola gravezza[35]: infatti scendono poco per volta ed insensibilmente, e cadendo non acquistano né impeto né impulso[36]. Il secondo suppone il falso, come dicevo: infatti se in una bilancia FH[37], il cui asse e centro è in G, da qui quindi si pongano due globi (appunto I e K) di egual peso, non si inclinerà la bilancia se si porrà uno di due in I, l’altro in L, infatti peserà ugualmente in L come in K[38]. La qual cosa stessa non potrà essere provata più efficacemente in nessun altro modo, che ricorrendo all’esperienza, maestra di tutte le cose.
Pag. 15[39] (foglio 35r)
L’ultima accusa costruita contro gli orologi meccanici, riguarda il peso della corda, che per quanto quella sia sottile, aggrava il peso. Si dimostra. Infatti nell’orologio MN[40] il peso è più[41] pesante in P che in O, poiché la corda NP è più lunga che NO. Quindi è anche più pesante. Quindi farà ruotare le ruote più velocemente. Questo ragionamento sembrò efficacissimo a Tycho, e lo sosteneva spesso con insistenza nelle lettere a Guglielmo langravio d’Assia, e al suo matematico Cristoforo Rothmann, che si servivano di orologi meccanici nel misurare il tempo. Ma questa non è stringente, poiché possiamo tracciare sul cerchio orario archi disuguali per le singole ore, se questa disuniformità fosse sensibile, come facemmo poco fa, quando per questa via ammettemmo in questo modo l’irregolarità della spira (del muelle), affinché non potesse neppure minimamente trarre in errore l’osservatore. Non voglio però entrare in questa via difficile e meno spedita e meno bella, è infatti praticabile un’altra facile. Considera l’orologio QR. Sia il peso in S. per esempio[42] sia anche abbassata ancora la corda dallo stesso peso fino allo stesso pavimento in T. dico che la corda, o il peso sia in S. sia in V. sarà uguale (appunto da R a T) è pertanto avrà uguale peso, e muoverà le ruote del meccanismo con uguale forza[43]. Questa verità è tanto manifesta e a portata di mano, che fui stupito nel frattempo, che non fosse venuta in mente a Tycho, uomo ingegnosissimo, né agli altri coi quali a partire da questo argomento fondamentale disputava contro l’affidabilità e la veridicità degli orologi meccanici.
[1] Hermann Wirekind non è corretto; nel foglio 33r Caramuel cita però un Hermann Witekind, che risulta avere scritto una “Conformatio Horologiorum” edita nel 1576 ad Heidelberg, il cui titolo completo è: Conformatio Horologiorum sciotericorum in superficiebus planis utcunque sitis, iacentibus, erectis, reclinatis, inclinatis, & quocunque spectantibus, compendiaria & facilis, Cum Quadrantis Horologici & Geometrici conformatione & vsibus, ac Tabulis Sinuum. Dall’opera di Witekind proviene effettivamente la citazione.
[2] Inizia qui la citazione da Witekind
[3] La frase greca è stata corretta eliminando gli errori grafici già contenuti nel testo di Witekind
[4] Si tratta di Giulio Polluce, sofista e grammatico greco (II sec. d. C.), che scrisse un Onomasticon in 10 libri, una specie di lessico ed elenco di sinonimi, giunto a noi in un ampio estratto, ordinato per argomenti.
[5] Qui finisce la citazione da Witekind
[6] Non è chiaro chi sia questo Federico al quale Caramuel si rivolge, e forse dedica l’opuscolo
[7] Cubito, come misura di lunghezza (corrispondente a circa 45 cm.)
[8] Si deve supporre che si riferisca al 1646, dato che Rodolfo II fu Imperatore del Sacro Romano Impero dal 1576 al 1612.
[9] Intende gli orologi meccanici, cioè quelli a ruote dentate
[10] Automi nel senso di “orologi meccanici”
[11] il testo continua sulla pag. 6, foglio 29r
[12] Dovrebbe essere Aldebaran (α Tauri o Alfa Tauri)
[13] Ottone
[14] Ho tradotto con “prassi” la parola “pragmatia” che non risulta presente nei dizionari di latino classico
[15] Ho introdotto un punto e virgola per separare due periodi
[16] Inizia qui la citazione da Alsted
[17] Ho tradotto con meccanici, avendo l’attuale espressione “orologio automatico” significato tecnico ben diverso da quello inteso da Caramuel
[18] Ho tradotto la frase di Caramuel sostituendo “propiora” al posto di “propria”. Con “propria” la frase non avrebbe senso. Si è operata la stessa correzione anche nella pagina successiva, dove Caramuel (o meglio il suo copista) cade nella stessa confusione dei due termini
[19] Finisce qui la citazione da Alsted
[20] La traduzione è basata sull’interpretazione dello scritto, non facilmente decifrabile, anche a causa delle abbreviazioni, come: “de fidelitate non omnia quae supra horologia dicuntur sunt vera”
[21] Hermann Witekind ha scritto una “Conformatio Horologiorum” edita nel 1576 ad Heidelberg
[22] Inizia qui la citazione da Witekind
[23] La parola “compassum” non compare nel latino classico; il fatto che si parli anche di un ago magnetico fa ritenere che si tratti di un orologio sciaterico dotato di bussola per orientarlo lungo il meridiano; questo confortato anche dal fatto che la bussola, in tedesco, è detta Kompass.
[24] Ho tradotto con “avvolgimento” e non con “torsione”, in considerazione della forma che le molle da orologio avevano già nel XVII sec.
[25] Caramuel intende “da noi spagnoli”
[26] Ho tradotto con “meccanico”, avendo la parola “automatico” un odierno significato ben diverso da quello che sembra intendere Caramuel
[27] Nel margine sinistro del foglio, in alto, è disegnata una figura, nella quale si riconoscono le lettere riportate nel testo. Vi si riconoscono due ruote dentate, delle quali la maggiore, ruotante intorno all’asse M, è unita ad una camma profilata ABC, sulla quale preme una molla DEF, fissata con chiodaura o spine (claviculi) in F.
[28] Uno spostamento delle virgole nel testo originale potrebbe attribuire “violentiâ et virtute” al retinaculum, con un senso più compiuto: ricondotta con la forza e la ragione di questo vincolo.
[29] Ho usato il linguaggio scientifico moderno della Meccanica Razionale.
[30] Dalla figura risulta conico
[31] Penso che si tratti del tendere e caricare la molla
[32] Dovrebbe riferirsi allo scorrere del tempo, anche se il defluire farebbe pensare alle clessidre, qui però non nominate
[33] Nella parte destra del foglio, la prima figura in alto mostra un quadrante d’orologio mostrante 12 ore disposte con spaziature differenti ed irregolari lungo l’angolo giro.
[34] Nel margine destro del foglio è disegnata una figura, la seconda dall’alto, nella quale si riconoscono i due orologi con le due diverse giaciture e le lettere riportate nel testo
[35] Ho usato la parola gravezza, nel senso di forza peso, per evitare l’uso della parola gravità, che sarebbe fuorviante, avendo un significato scientifico che non esisteva al tempo di Caramuel. Non è facilmente comprensibile cosa intenda Caramuel con “impulsu secundario”, forse l’equivalente dell’energia cinetica, o della quantità di moto, concetti allora sconosciuti
[36] Probabilmente con “impulsus” Caramuel intende slancio, abbrivio
[37] A destra si trova la figura di una bilancia, con fulcro in G, ed estremità dei bracci contrassegnate con F ed H
[38] Osservando la figura, quella più in basso delle altre, e conoscendo le leggi della leva, già note dai tempi di Archimede, si può capire come con alter Caramuel intenda il secondo peso (l’altro tra due), che può essere spostato indifferentemente da K a L
[39] La pag. 15 si trova nella parte destra dello stesso foglio della pag. 14, dalla quale è separata dalle figure
[40] A sinistra si trova la figura di due orologi, quello più a sinistra contrassegnato con MN, quello più a destra con QR
[41] Il testo riporta “gravis est pondus in P, quàm in O”: deve correggersi “gravis” con “gravius” per rendere il senso del confronto fatto da Caramuel.
[42] Ho tradotto con “per esempio”, supponendo che “ex. gr.” stia per “exempli gratia”
[43] Caramuel disegna una corda che, scendendo dall’orologio in R, si appoggia sul pavimento (si veda nel disegno la corda che si appoggia con andamento serpentiforme). Caramuel trascura però che la flessibilità della corda non è perfetta né ideale.
